Overview / Logistics

The purpose of this problem set is to give you practice with NFAs and their interplay with DFAs. At the heart of what we're doing is the idea that if we've done the hard work to design DFAs to recognize some language(s), we can do a little more work to treat them as modules and to combine them in clever ways to make DFAs that recognize other languages. Sometimes an NFA will help as an intermediate step.

For all problems that require you to construct an NFA or a DFA, you should submit a JFLAP file. For all other problems, submit a picture of pen + paper work or a PDF document of a writeup. Enjoy!

Problem 1: The Union of Regular Languages (3 Points)

Design a DFA that recognizes strings that are divisible by 3 OR divisible by 4. Then, design an NFA that also recognizes this language

Below are some tests you can try in JFLAP (Click here to download them)

Decimal Number	Input	Result
44	101100	Accept
47	101111	Reject
64	1000000	Accept
67	1000011	Reject
67	1000011	Reject
9	1001	Accept
83	1010011	Reject
21	10101	Accept
36	100100	Accept
87	1010111	Accept

Problem 2: The Intersection of Regular Languages (3 Points)

Prove by construction that regular languages are closed under intersection

Hint: You can do a similar construction to the proof that regular languages are closed under union, but all you need to change is the accept state

Problem 3: NFA Design (3 Points)

Design an NFA that recognizes the language of odd binary numbers that have a 1 in the 32s place, when read from left to right.

Below are some tests you can try in JFLAP (Click here to download them)

Decimal Number	Input	Result
99	1100011	Accept
206	11001110	Reject
239	11101111	Accept
189	10111101	Accept
230	11100110	Reject
118	1110110	Reject
144	10010000	Reject
73	1001001	Reject
8	1000	Reject
228	11100100	Reject

Problem 4: The Complement of Regular Languages (3 Points)

We've seen some examples where swapping the accept and non-accept states of a DFA that recognizes a language L over the alphabet Σ yields a DFA which recognizes the complement of L; that is, all strings made up of characters from Σ that are not in L. For instance, the machine below accepts binary strings that contain 1010 somewhere (Click here for the JFLAP file)

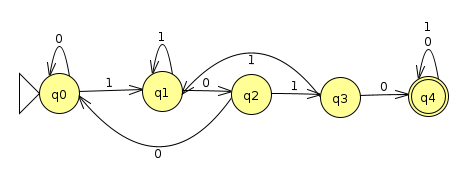
and the machine below accepts binary strings that do not contain 1010 (Click here for the JFLAP file)

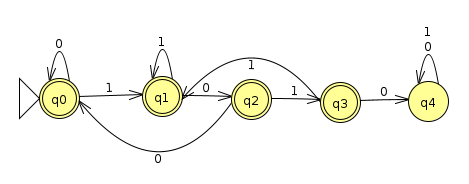
Does this same property hold for NFAs? If so, provide a proof in general. If not, show a counter-example (an example where this is not true), along with the inputs that break it.

Problem 5: The Union And Concatenation of Regular Languages (3 Points)

Create an NFA that recognizes the the language of strings with a nonzero and even number of a's or with a nonzero and even number of bs, followed by one or more bs, followed by an odd number of a's or an odd number of b's.

Below are some tests you can try in JFLAP (Click here to download them). If you don't agree on a particular test case, take advantage of JFLAP's NFA branch explorer by trying that test out with Input->Step By State

Input	Result
aaaab	Reject
bbaabbb	Accept
bbaabaa	Reject
aabbbb	Accept
ababab	Accept
abab	Reject
ababb	Accept
aaaba	Reject
bbb	Reject
bbbb	Accept
bbbbbbbbbbbbbb	Accept
aaaaaaaaaaa	Reject
bbbaabb	Accept

Let's highlight a couple of the accept strings to show how they get split up

Example 1: ababab

We can split this up as follows

A nonzero and even number of a's or with a nonzero and even number of bs	One or more bs	An odd number of a's or an odd number of b's
aba	b	ab

Example 2: ababb

A nonzero and even number of a's or with a nonzero and even number of bs	One or more bs	An odd number of a's or an odd number of b's
aba	b	b

Example 3: bbbbbbbb

There are a bunch of ways to split this one up.

A nonzero and even number of a's or with a nonzero and even number of bs	One or more bs	An odd number of a's or an odd number of b's
bb	bbb	bbb
bbbb	b	bbb
bb	bbbbb	b

Problem 6: The Reverse of Regular Languages Part 1 (3 Points)

Prove using a DFA that if a binary string is divisible by 3, then its reverse is also divisible by 3.

Problem 7: The Reverse of Regular Languages Part 2 (3 Points)

If a binary string is divisible by 6, then its reverse is not necessarily divisible by 6. For instance, the string 1100 (12) is divisible by 6, but its reverse 0011 (3) is not divisible by 6. Construct a DFA that recognize the language of binary strings whose reverse is divisible by 6. These strings should be inputted from right to left.

Hint: First construct and test an NFA that recognizes this language, then convert this to a DFA using the technique we described in class. If you've only expanded the states you needed to expand, the DFA should have even fewer states than the one that recognizes strings divisible by 6!

Below are some tests you can try in JFLAP (Click here to download them)

Input	Decimal Number	Reverse Binary	Reverse Decimal	Result
1010111	87	1110101	117	Reject
00100001	33	10000100	132	Accept
001101	13	101100	44	Reject
00000011	3	11000000	192	Accept
0010011	19	1100100	100	Reject
0110011	51	1100110	102	Accept
01101111	111	11110110	246	Accept
11010111	215	11101011	235	Reject
0010101	21	1010100	84	Accept
00010001	17	10001000	136	Reject

Problem 8: DFAs for Substring Search (5 Points)

We're going to examine an application of DFAs that's used all the time behind the scenes in text editors and web browsers. Consider the following problem: given a string pattern and a string s, determine if pattern is a substring (contiguous subset) of s. One way to do this is to check every possible subset of length len(pattern) in s. The code below shows how one might do this in python:

So, for instance, if we run

We should get [14, 20] (zero-indexed), since the pattern shows up twice at the end. However, our algorithm goes quite slow on this because there are many times where it almost matches the pattern, but then it has to start over. In the worst case, this algorithm can take len(pattern)*len(s) steps, so we say it's a O(len(pattern)*len(s)) algorithm (we will talk about big-O notation later in the course).

As it turns out, we can construct a DFA for substring that only has to go through each character in the string exactly once, and we report a match every time it reaches an accept state. Hence, the algorithm only takes O(len(s)) time, which can be substantially better in practice if pattern is long. For instance, consider the following DFA (Click here to download the JFLAP file)

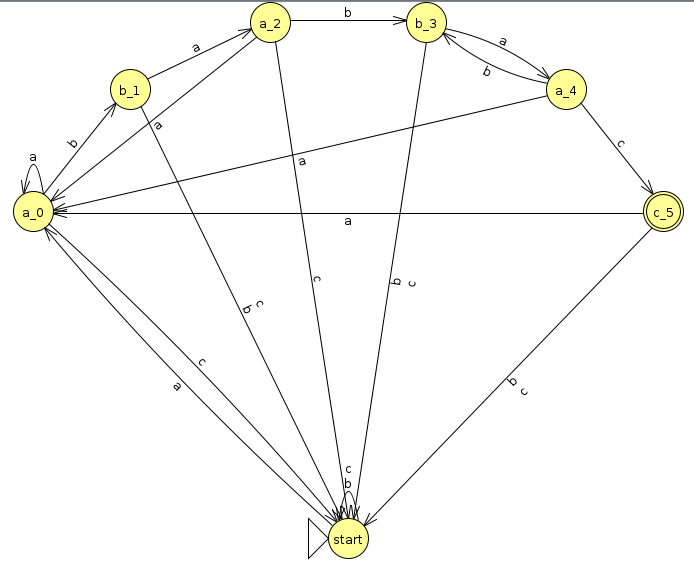
Now let's step through and search for our pattern:

You'll notice that we reached the accept state exactly twice at the end of each instance of pattern in s. But how on earth did we come up with this? Here is a fairly straightforward algorithm to do this:

Algorithm 1: Straightforward Substring DFA Creation

1. Create a state start and a state c_i for each character c in the pattern at index i. For instance, if the pattern is acdc, you should have the states
   • start
   • a_0
   • c_1
   • d_2
   • c_3

2. Add state transitions for the matched characters in sequence. For instance, in the acdc pattern, we'd have a transition from start to a_0 when we see an a, a transition from a_0 to c_1 when we see a c, etc.

   Also, in a separate loop, add the remaining arrows from start back to itself for all other characters in the alphabet. In acdc, assuming an alphabet of {a, b, c, d}, we'd add the arrows from b, c, and d from start to itself.

3. Loop through each character in the pattern in sequence. For each character c at index i, loop through all characters a in the alphabet Sigma.
   • If an arrow doesn't exist yet at ci using a,
     • Then the first i+1 characters of pattern do not match the string where we are ending at a
     • However, it is possible that the last i characters of the string match the first i characters of the pattern, or that the last i-1 characters of the pattern match the first i-1 characters of the pattern, etc.
     . To figure out how much of the pattern we've actually matched, send a concatenated to the last i characters of pattern (pattern[1:i+1]+a in python) through the DFA that you've built so far, and use the state that you end on as the transition out of ci through a

Your task

Click here to download the starter code for this task.

Create a python method make_substring_dfa(Sigma, pattern) that takes in an alphabet as a list in Sigma and a pattern string, and which returns a delta dictionary describing the DFA transitions that match pattern. For example, if you run the following code:

So, for instance, if you run then your program should output the above example. It will also print the values of the dictionary, which you can check individually. They should look like this on the above example, in no particular order:

Hint

The following code will create the strings representing the states for each character c at index i

Hint 2

If you're having trouble figuring out where to get started, at least see if you can do step 1 in the algorithm, then save the DFA and look at it in JFLAP to see if you have the right states. Then try step 2 and see if you have the arrows for matching characters. Finally, you can tackle the third step, which is the hardest

Extra Credit (+2)

The DFA that you've built is very efficient and can find all instances of the pattern in O(len(s)) time, which is substantially better than the O(len(s)*len(pattern)) algorithm we started with. However, algorithm 1 for constructing the DFA is not very efficient, and is in fact O(len(alphabet)*len(pattern)2), assuming a constant alphabet size, which is quite bad for long patterns. Luckily, there is a variation that we can do known as the Knuth-Morris-Pratt algorithm to accomplish DFA construction with all arrows in O(len(alphabet)*len(pattern)) time only. Implement this algorithm to construct your DFA instead of the one described in algorithm 1. Click here to view some notes about this on GeeksForGeeks.

NOTE: In practice, the KMP algorithm doesn't actually store arrows for every character in the alphabet coming out of each state; it only tells you where to jump if there's about to be a mismatch, before you process the next character. This is more efficient to do in practice, because it scales well for large alphabets. What I'm looking for in the extra credit, though, is to create all arrows using a similar trick to what KMP does. In particular, you'll want to track the longest suffix of the string you're searching that's still a prefix of the pattern you're matching, rather than checking the entire suffix minus one character like we've been doing.