Today we discussed formal descriptions of DFAs. What we learned is that a DFA can be described as a "5-tuple" (Q, Σ, δ, q, F). The meaning of each of these terms is as follows

• Q: A set of all of the states in the DFA
• Σ: A set of all characters in the alphabet
• δ: A function describing the arrows in the diagram. The function is of the form

  \[ \delta: Q \times \Sigma \to Q \]

  That is, it takes tuples of (state, character) and returns a state
• q: The start state
• F: A set of the accept states or "final states"

Note that the start state q is a single element, because we can only have one start state, and the accept states are actually in a set because there can be multiple of them

Example 1

It's easiest to see what these are with an example. Let's consider the following DFA that accepts all binary strings containing 001 (Click here for the JFLAP file)

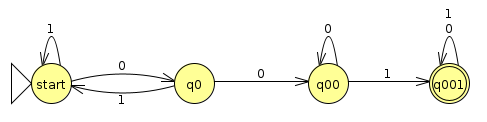
Below is a table showing the definition of the 5-tuple for this DFA

Q	{start, q0, q00, q01}
Σ	{0, 1}
δ	0 1 start q0 start q0 q00 start q00 q00 q001 q001 q001 q001
q	start
F	{q001}

Note that while it's convenient to define δ as a table, we will sometimes hone in on particular inputs of the function with the notation δ(state, symbol). For instance, δ(q00, 1) = q001 in this example

Example 2

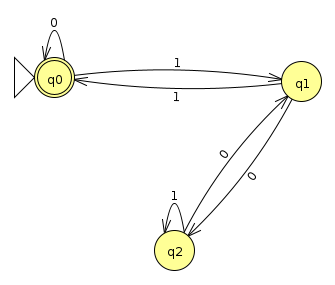
In this example, we'll go the other way around; that is, given a 5-tuple, we'll create a state diagram that realizes it visually. The 5-tuple is as follows

Q	{q0, q1, q2}
Σ	{0, 1, 2}
δ	0 1 2 q0 q0 q1 q2 q1 q1 q2 q0 q2 q2 q0 q1
q	q0
F	{q0}

Below is the picture we came up with in class for this (Click here to download the JFLAP file)

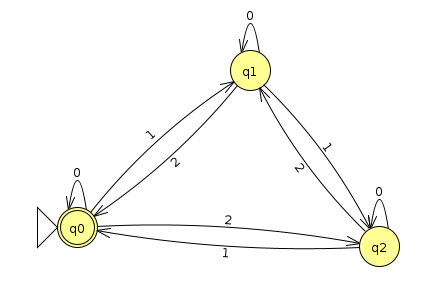
Notice how there are actually three arrows coming out of each state since there are three symbols in the alphabet Σ. As for an interpretation of this machine, the one I had in mind was that it would accept a string of 0s, 1s, and 2s whose sum was divisible by 3 (i.e. had a zero remainder).

Example 3

So why the big deal about this formal notation? Well, it makes it easier for us to specify more huge machines or more general classes machines more succinctly and without having to draw them. Let's consider an example of a machine that accepts a binary string with at most K zeros, where K here is left open as a variable. We couldn't draw this as a picture in general (unless we wanted to draw infinitely many pictures: one for each case). But we can describe it symbolically:

Q	{q0, q1, q2, ..., qK, qK+1}
Σ	{0, 1}
δ	We'll split this definition into two cases: //This case moves us to the right if we've seen another zero, or stays where we are if we see a 1 If i <= k, then δ(qi, 0) = qi+1 δ(qi, 1) = qi //Once we've seen more than K zeros, we can stay where we are at the "invalid" state qK+1 δ(qK+1, 0) = qK+1 δ(qK+1, 1) = qK+1
q	q0
F	{q0, q1, ..., qK} //Any state accepts, as long as it's not more than K zeros

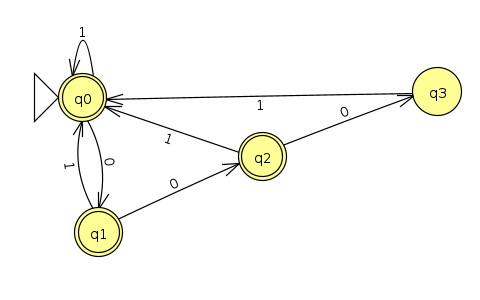
For example, when K=2, we have the following DFA (Click here to download the corresponding JFlap files):

Example 4

Let's do one more example where formal notation is handy. Consider a machine that accepts binary strings representing numbers that are divisible by 2^K. This means that the binary strings have to either be all 0, or they have to end in K zeros. For instance, divisibility by 2²=4 would have to either be 0 or end in 2 zeros. A machine handling this case is shown below (Click here to download the JFLAP file)

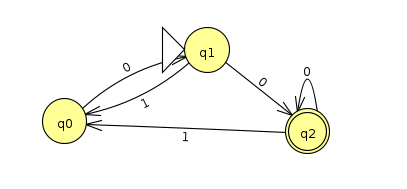
A general strategy for ending in K zeros is to create a machine with K+1 states q₀, ..., q_K-1, q_K, where the index counts how many zeros have been seen, and to start at q_K-1:

Q	{q0, q1, q2, ..., qK, qK}
Σ	{0, 1}
δ	If i < k, then δ(qi, 0) = qi+1 δ(qi, 1) = q0 δ(qK, 0) = qK δ(qK, 1) = q0
q	qK-1
F	{qK}

---

Formal Languages: Definitions

We now have the terminology we need to formally define what is meant by a regular language. We'll need a few other definitions first

For instance, the set of all binary strings ending in 1 is a language over the alphabet Σ = {0, 1}.

Notice how there is one more element in the accepting sequence than there is in the string. This is because we start at the start state before we process any characters.

As a sanity for the notation, it's sometimes helpful to look through an example and plug in some numbers. If we look back at example 2 and we're given the string 112122, then we can give the sequence q0, q1, q2, q1, q2, q1, q0, and the 3 conditions above will be satisfied. The diagram below shows an "unrolling" of the state sequence, with arrows showing a transition from one state to the enxt for each character.

Looking at it this way, it should perhaps also be clear why there's always one more state in the sequence (we index the states starting at r₀) than there are characters in the string (we index the string starting at w₁).

Let's now proceed to a formal definition of what it means for a DFA to recognize a language

We're now finally ready to define a regular language

At this point, you may wonder if all languages are regular. Certainly if we can design a DFA, then it implies a language that is regular, so that encompasses everything we've looked at in this class so far. However, there are certain languages that are not regular. For instance, the language of all binary palindromes (e.g. 10111101, 10000001, 1101111011), is not regular. It seems like it would be tough to prove, because we'd somehow have to rule out infinitely many possible DFAs we could consider! But next week we will go over some tricks to show that certain proposed languages are not regular.

---

Formal Regular Languages: Code

Let's revisit some of the python code from week 1, because we will see that it corresponds almost exactly to the formal definitions we had above. Let's consider a DFA that accepts binary strings with an odd number of 1's. Here's how we would specify this machine formally using python sets and dictionaries:

And here's how we would check if a particular string s is in recognized by the DFA, which matches nearly exactly the definition of DFA acceptance that we had:

---

Binary Divisibility Checks

You have a problem on your problem set about divisibility by 5 of binary numbers read from left to right. You will prove by construction that the set of all binary numbers divisible by 5 form a regular language.

In the meantime, as an example, let's complete the divisibility by 3 example to elucidate a strategy that can be used to design DFAs for general divisibility. This time I'll actually give the solution first and then I'll explain it. Below is a state diagram that accomplishes this in JFLAP (Click here to download the JFLAP file)

As a sanity check, we see that 3 (binary 11), 6 (binary 110), 9 (binary 1001), 12 (binary 1100), and 15 (binary 1111) are accepted. But how the heck do we come up with this?

First, we use the fact that all numbers have either a remainder of 0, 1, or 2 when divided by 3. We'll make a state for each of these possibilities and move between them as we get more information. If we stop at the remainder 0 state, then we accept, since that implies it's evenly divisible by 3

Now, to come up with the transitions, we have to think about what happens when we get an addition bit of information from left to right. What this means is what we thought we had actually shifts over to the left by 1 place. A binary left shift is actually multiplication by 2, just like shifting the digits of an ordinary base 10 number to the left is like multiplying by 10. So we can use this fact to help us. For instance, if we had the string 111 and were in the divisible by 1 state, and then we got a new bit b, the string we now have would be 111b. Our new string is then 1110 + b. If b = 0, then we move to the divisible by 2 state. If b = 1, then we move to the divisible by 0 state.

To treat the state transitions in general, we consider the three cases

• If we currently have a remainder of 0, that means our number is 3k for some natural number k. We get a new bit b and shift to the left, which makes this 6k + b. 6k divides evenly by 3, so that part doesn't matter, and we are just left with b. So if b = 0, we stay with a remainder of 0, and if b = 1, we have a remainder of 1
• If we currently have a remainder of 1, that means our number is 3k + 1. We get a new bit b and shift this to the left, and it turns into 2(3k+1) + b = 6k + 2 + b. Again, the 6k part drops out, and we're just left with 2+b. We see then if b = 0, we move to be divisible by 2, and if b = 1, we move to be divisible by 0
• If we currently have a remainder of 2, that means our number is 3k + 2. We get a new bit b and shift this to the left, and it turns into 2(3k+2) + b = 6k + 4 + b. Again, the 6k part drops out, and we're just left with 4+b, which we can remove a factor of 3 from to get 1 + b. We see then if b = 0, we move to be divisible by 1, and if b = 1, we stay divisible by 2.

---

Languages with A Finite Number of Finite Strings are Regular

As another example, we can prove that any language with a finite set of finite strings is regular. For example, the language {0, 1, 01} is regular. Below is a DFA that recognizes it (Click here for the JFLAP file):

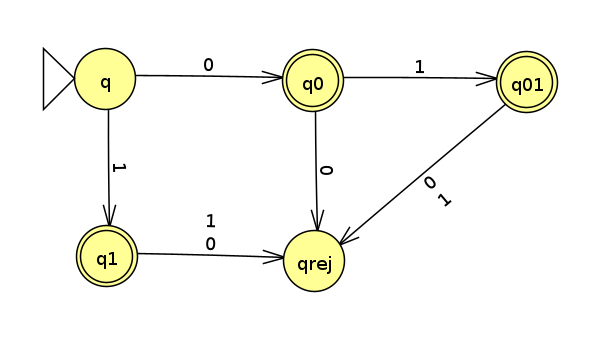
Proof

I'm expanding on an idea that Breeze Tucker had in class. We will do a proof by construction where we design a DFA to recognize any language L = {s₁, s₁, ..., s_N}, where each string is finite, is as follows:

1. Let d be the length of the longest string in L
2. Create a binary tree of depth d, with 2^d+1-1 nodes total, where each node is a state, and transition arrows coming out of each node go to its left child on a 0 and its right child on a 1.
3. Make the root of the tree be the start state
4. Mark each state as an accept state if we reach that state for a particular string in L
5. Add one additional "reject state" that all strings beyond length d go to and stay. This makes 2^d nodes total.

For fun, I've written some code to automatically generate these trees in JFLAP. Click here to view this code. I used it to generate a few examples below:

3 Short Strings Example

We'll redo the language {0, 1, 01} using this technique. The result is shown below (Click here for the JFLAP file).

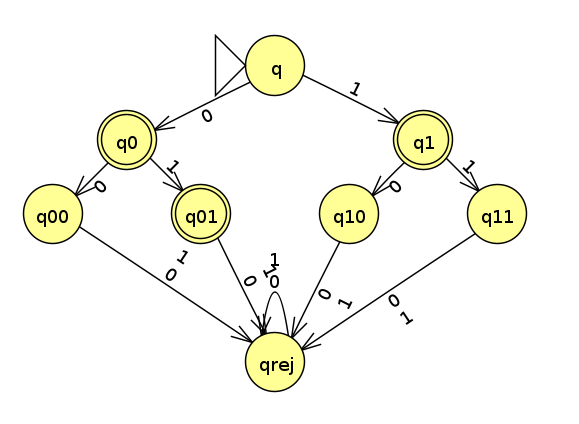
We see this is not as efficient as the machine we came up with before, but efficiency doesn't really matter in this context, because we're just trying to show the existence of a DFA that recognizes a language; it doesn't have to be the best one.

Binary Palindromes ≤= 5

A string is a palindrome if it is the same read forwards and backwards. The machine below recognizes the language of binary strings that are palindromes with at most 5 characters: (Click here to see the JFLAP file)

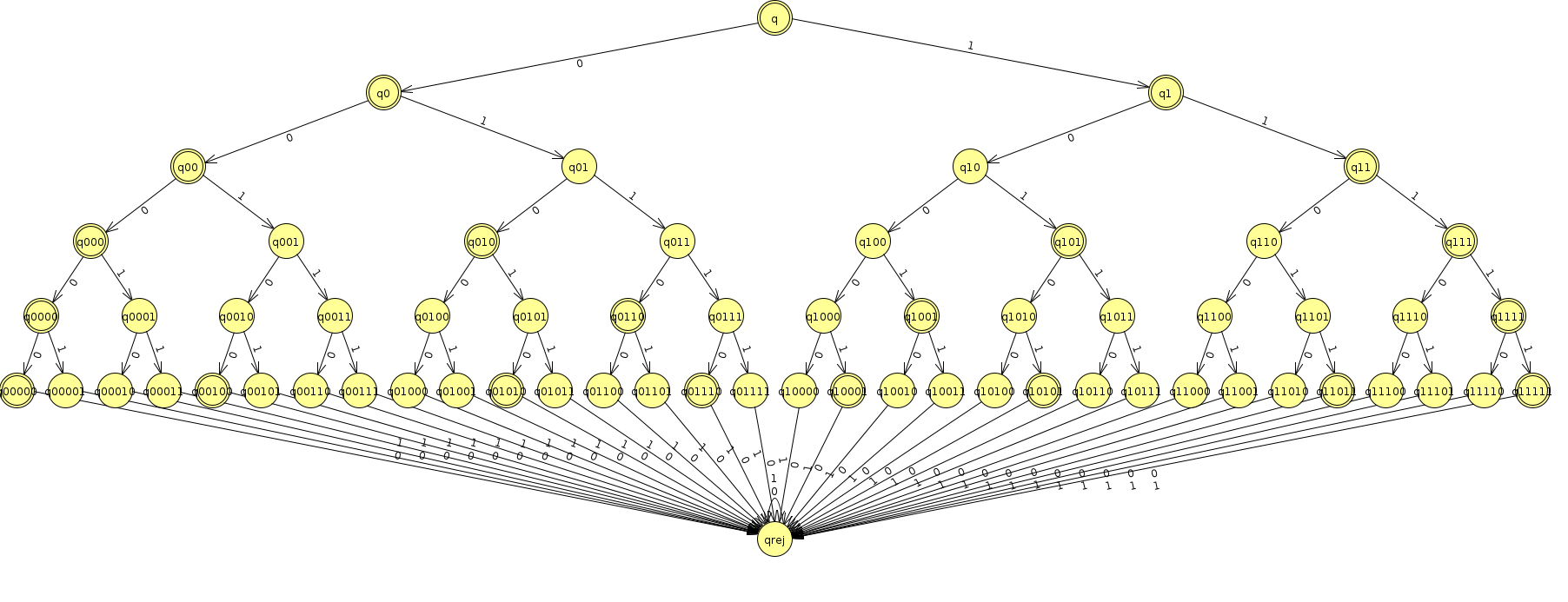
Interestingly, as we will prove later, the languages of palindromes of arbitrary length is not regular, but if put a cap on the length, they are!