Homework 3: NFAs And DFAs (26 Points)
Chris Tralie
Overview / Logistics
The purpose of this problem set is to give you practice with NFAs and their interplay with DFAs. At the heart of what we're doing is the idea that if we've done the hard work to design DFAs to recognize some language(s), we can do a little more work to treat them as modules and to combine them in clever ways to make DFAs that recognize other languages. Sometimes an NFA will help as an intermediate step.
For all problems that require you to construct an NFA or a DFA, you should submit a JFLAP file. For all other problems, submit a picture of pen + paper work or a PDF document of a writeup. Enjoy!
Problem 1: The Union of Regular Languages (3 Points)
Design a DFA that recognizes strings that are divisible by 3 OR divisible by 4. Then, design an NFA that also recognizes this language
Below are some tests you can try in JFLAP (Click here to download them)
| Decimal Number | Input | Result |
| 44 | 101100 | Accept |
| 47 | 101111 | Reject |
| 64 | 1000000 | Accept |
| 67 | 1000011 | Reject |
| 67 | 1000011 | Reject |
| 9 | 1001 | Accept |
| 83 | 1010011 | Reject |
| 21 | 10101 | Accept |
| 36 | 100100 | Accept |
| 87 | 1010111 | Accept |
Problem 2: The Intersection of Regular Languages (3 Points)
Prove by construction that regular languages are closed under intersection
Hint: You can do a similar construction to the proof that regular languages are closed under union, but all you need to change is the accept state
Problem 3: NFA Design (3 Points)
Design an NFA that recognizes the language of odd binary numbers that have a 1 in the 32s place, when read from left to right.
Below are some tests you can try in JFLAP (Click here to download them)
| Decimal Number | Input | Result |
| 99 | 1100011 | Accept |
| 206 | 11001110 | Reject |
| 239 | 11101111 | Accept |
| 189 | 10111101 | Accept |
| 230 | 11100110 | Reject |
| 118 | 1110110 | Reject |
| 144 | 10010000 | Reject |
| 73 | 1001001 | Reject |
| 8 | 1000 | Reject |
| 228 | 11100100 | Reject |
Problem 4: The Complement of Regular Languages (3 Points)
We've seen some examples where swapping the accept and non-accept states of a DFA that recognizes a language L over the alphabet Σ yields a DFA which recognizes the complement of L; that is, all strings made up of characters from Σ that are not in L. For instance, the machine below accepts binary strings that contain 1010 somewhere (Click here for the JFLAP file)
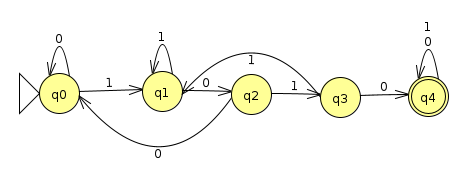
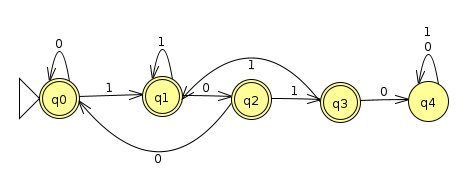
and the machine below accepts binary strings that do not contain 1010 (Click here for the JFLAP file)
Does this same property hold for NFAs? If so, provide a proof in general. If not, show a counter-example (an example where this is not true), along with the inputs that break it.
Problem 5: The Union And Concatenation of Regular Languages (3 Points)
Create an NFA that recognizes the the language of strings with a nonzero and even number of a's or with a nonzero and even number of bs, followed by one or more bs, followed by an odd number of a's or an odd number of b's.
Below are some tests you can try in JFLAP (Click here to download them). If you don't agree on a particular test case, take advantage of JFLAP's NFA branch explorer by trying that test out with Input->Step By State
| Input | Result |
| aaaab | Reject |
| bbaabbb | Accept |
| bbaabaa | Reject |
| aabbbb | Accept |
| ababab | Accept |
| abab | Reject |
| ababb | Accept |
| aaaba | Reject |
| bbb | Reject |
| bbbb | Accept |
| bbbbbbbbbbbbbb | Accept |
| aaaaaaaaaaa | Reject |
| bbbaabb | Accept |
Let's highlight a couple of the accept strings to show how they get split up
Example 1: ababab
We can split this up as follows
| A nonzero and even number of a's or with a nonzero and even number of bs | One or more bs | An odd number of a's or an odd number of b's |
| aba | b | ab |
Example 2: ababb
| A nonzero and even number of a's or with a nonzero and even number of bs | One or more bs | An odd number of a's or an odd number of b's |
| aba | b | b |
Example 3: bbbbbbbb
There are a bunch of ways to split this one up.
| A nonzero and even number of a's or with a nonzero and even number of bs | One or more bs | An odd number of a's or an odd number of b's |
| bb | bbb | bbb |
| bbbb | b | bbb |
| bb | bbbbb | b |
Problem 6: The Reverse of Regular Languages Part 1 (3 Points)
Prove using a DFA that if a binary string is divisible by 3, then its reverse is also divisible by 3.
Problem 7: The Reverse of Regular Languages Part 2 (3 Points)
If a binary string is divisible by 6, then its reverse is not necessarily divisible by 6. For instance, the string 1100 (12) is divisible by 6, but its reverse 0011 (3) is not divisible by 6. Construct a DFA that recognize the language of binary strings whose reverse is divisible by 6. These strings should be inputted from right to left.
Hint: First construct and test an NFA that recognizes this language, then convert this to a DFA using the technique we described in class. If you've only expanded the states you needed to expand, the DFA should have even fewer states than the one that recognizes strings divisible by 6!
Below are some tests you can try in JFLAP (Click here to download them)
| Input | Decimal Number | Reverse Binary | Reverse Decimal | Result |
| 1010111 | 87 | 1110101 | 117 | Reject |
| 00100001 | 33 | 10000100 | 132 | Accept |
| 001101 | 13 | 101100 | 44 | Reject |
| 00000011 | 3 | 11000000 | 192 | Accept |
| 0010011 | 19 | 1100100 | 100 | Reject |
| 0110011 | 51 | 1100110 | 102 | Accept |
| 01101111 | 111 | 11110110 | 246 | Accept |
| 11010111 | 215 | 11101011 | 235 | Reject |
| 0010101 | 21 | 1010100 | 84 | Accept |
| 00010001 | 17 | 10001000 | 136 | Reject |
Problem 8: DFAs for Substring Search (5 Points)
We're going to examine an application of DFAs that's used all the time behind the scenes in text editors and web browsers. Consider the following problem: given a string pattern and a string s, determine if pattern is a substring (contiguous subset) of s. One way to do this is to check every possible subset of length len(pattern) in s. The code below shows how one might do this in python:
So, for instance, if we run
We should get [14, 20] (zero-indexed), since the pattern shows up twice at the end. However, our algorithm goes quite slow on this because there are many times where it almost matches the pattern, but then it has to start over. In the worst case, this algorithm can take len(pattern)*len(s) steps, so we say it's a O(len(pattern)*len(s)) algorithm (we will talk about big-O notation later in the course).
As it turns out, we can construct a DFA for substring that only has to go through each character in the string exactly once, and we report a match every time it reaches an accept state. Hence, the algorithm only takes O(len(s)) time, which can be substantially better in practice if pattern is long. For instance, consider the following DFA (Click here to download the JFLAP file)
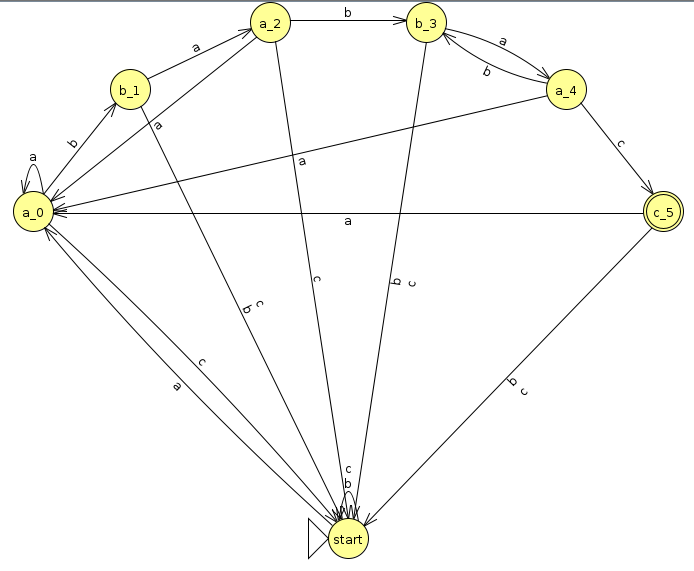
Now let's step through and search for our pattern:

You'll notice that we reached the accept state exactly twice at the end of each instance of pattern in s. But how on earth did we come up with this? Here is a fairly straightforward algorithm to do this:
Algorithm 1: Straightforward Substring DFA Creation
-
Create a state
startand a statec_ifor each charactercin the pattern at indexi. For instance, if the pattern isacdc, you should have the states-
start -
a_0 -
c_1 -
d_2 -
c_3
-
-
Add state transitions for the matched characters in sequence. For instance, in the
acdcpattern, we'd have a transition fromstarttoa_0when we see ana, a transition froma_0toc_1when we see ac, etc.Also, in a separate loop, add the remaining arrows from start back to itself for all other characters in the alphabet. In
acdc, assuming an alphabet of{a, b, c, d}, we'd add the arrows from b, c, and d from start to itself. -
Loop through each character in the pattern in sequence. For each character
cat indexi, loop through all charactersain the alphabetSigma.-
If an arrow doesn't exist yet at
ciusinga,-
Then the first
i+1characters ofpatterndo not match the string where we are ending ata -
However, it is possible that the last
icharacters of the string match the firsticharacters of the pattern, or that the lasti-1characters of the pattern match the firsti-1characters of the pattern, etc. .
To figure out how much of the pattern we've actually matched, send
aconcatenated to the lasticharacters of pattern (pattern[1:i+1]+ain python) through the DFA that you've built so far, and use the state that you end on as the transition out ofcithrough a -
Then the first
-
If an arrow doesn't exist yet at
Your task
Click here to download the starter code for this task.
Create a python method make_substring_dfa(Sigma, pattern) that takes in an alphabet as a list in Sigma and a pattern string, and which returns a delta dictionary describing the DFA transitions that match pattern. For example, if you run the following code:
Hint
The following code will create the strings representing the states for each character c at index i
Hint 2
If you're having trouble figuring out where to get started, at least see if you can do step 1 in the algorithm, then save the DFA and look at it in JFLAP to see if you have the right states. Then try step 2 and see if you have the arrows for matching characters. Finally, you can tackle the third step, which is the hardest
Extra Credit (+2)
The DFA that you've built is very efficient and can find all instances of the pattern in O(len(s)) time, which is substantially better than the O(len(s)*len(pattern)) algorithm we started with. However, algorithm 1 for constructing the DFA is not very efficient, and is in fact O(len(alphabet)*len(pattern)2), assuming a constant alphabet size, which is quite bad for long patterns. Luckily, there is a variation that we can do known as the Knuth-Morris-Pratt algorithm to accomplish DFA construction with all arrows in O(len(alphabet)*len(pattern)) time only. Implement this algorithm to construct your DFA instead of the one described in algorithm 1. Click here to view some notes about this on GeeksForGeeks.
NOTE: In practice, the KMP algorithm doesn't actually store arrows for every character in the alphabet coming out of each state; it only tells you where to jump if there's about to be a mismatch, before you process the next character. This is more efficient to do in practice, because it scales well for large alphabets. What I'm looking for in the extra credit, though, is to create all arrows using a similar trick to what KMP does. In particular, you'll want to track the longest suffix of the string you're searching that's still a prefix of the pattern you're matching, rather than checking the entire suffix minus one character like we've been doing.