It's now time to consider some languages that are not decidable. If a language L is not decidable, it means that while it may be possible to design a Turing machine to recognize L, we can't hope to avoid an infinite loop on all strings not in the language.

We'll start with a very specific example of an undecidable language known as A_TM, which we will use as the canonical undecidable language when proving that other languages are undecidable. It will be one very short step after this to prove that the ever famous Halting problem is undecidable, but that is just the tip of the iceberg of interesting problems we can't hope to solve in general, as we will see 😿😿😿.

---

A_TM Is Undecidable

We define a language called A_TM which is the Turing machine version of A_DFA and A_CFG

A_TM = {<M,w> | M is a Turing machine and M accepts the string w}

Claim: Unlike A_DFA and A_CFG, however, A_TM is not decidable.

Proof: Intuitively, there's something about the fact that Turing machines can throw infinite loops that prevent us from being able to rule out a particular string from just taking a long time to accept/reject or from actually infinitely looping. But we need a more rigorous argument for this.

Suppose by contradiction that A_TM is actually decidable, and let a decider for it be a machine called A. Then we can use A as a subroutine to build another decidable universal Turing machine which I'll call weird (following Thorsten Altenkirch's convention). Below is a high level description of this machine, which feeds a string encoding of M to itself:

In other words, weird does the opposite of A on the string encoding of a machine and itself. Since A is assumed to be a decidable Turing machine, so is weird. But here's a diagonalization argument can run us into trouble. Since the set of all Turing machines is countable, we can arrange all possible Turing machines along the rows of a table in some order (such as the lexographic order of their string encoding). We'll then order their string encodings in the same order across the columns. In the entries of the table, let's record Accept or Reject to indicate whether the machine on the row accepts or rejects the string encoding of the machine on the column. Since we've assumed that A_TM is decidable, then these are the only two possibilities for its decider A. For instance, here's that table on six arbitrary Turing machines M₁ ... M₆

	<M1>	<M2>	<M3>	<M4>	<M5>	<M6>	...
M1	Accept	Accept	Accept	Reject	Accept	Accept	...
M2	Accept	Accept	Reject	Accept	Accept	Accept	...
M3	Accept	Accept	Accept	Accept	Accept	Reject	...
M4	Accept	Reject	Accept	Reject	Reject	Reject	...
M5	Accept	Accept	Accept	Accept	Reject	Accept	...
M6	Accept	Accept	Reject	Accept	Accept	Accept	...
...	...	...	...	...	...	...	...

But we just argued a moment ago that weird is a valid Turing machine, so we should be able to have a row and column for weird and its string encoding <weird>, respectively, in our table. Since weird does the reverse behavior of A on a machine and its string encoding, the value of weird's row at the i^th column should be the opposite of the i^th diagonal entry of the table. Let's try to do this:

	<M1>	<M2>	<M3>	<M4>	<M5>	<M6>	...	<weird>	...
M1	Accept	Accept	Accept	Reject	Accept	Accept	...	Reject	...
M2	Accept	Accept	Reject	Accept	Accept	Accept	...	Reject	...
M3	Accept	Accept	Accept	Accept	Accept	Reject	...	Reject	...
M4	Accept	Reject	Accept	Reject	Reject	Reject	...	Accept	...
M5	Accept	Accept	Accept	Accept	Reject	Accept	...	Reject	...
M6	Accept	Accept	Reject	Accept	Accept	Accept	...	Accept	...
...	...	...	...	...	...	...	...	...	...
weird	Reject	Reject	Reject	Accept	Accept	Reject	...	🙀🙀???🙀🙀	...
...	...	...	...	...	...	...	...	...	...

We start off just fine by having weird do the opposite on other machines. However, when we get to weird itself, we reach a contradiction, because we define its accept/reject status to be the opposite of what it is. But it's impossible to choose either accept or reject to be the opposite of itself. So we've arrived at a contradiction. The only falsifiable assumption we made this whole time is that A_TM is decidable. Therefore, A_TM must not be decidable!

Diagonalization Disclaimer!!

Most math students would be used to using a diagonalization argument to prove that certain sets are uncountably infinite. But that's not what we're showing with A_TM! Actually, as we discussed, the set of all strings in an alphabet is countably infinite, and every language is a subset of these strings, so every language must be countable, whether it's decidable or not. So even though A_TM is undecidable, it is still countably infinite! So don't make the mistake of assuming that undecidable languages are uncountable!

At the root of the confusion is exactly what we're assuming by contradiction before we apply the diagonal argument. When we prove that a set is uncountable, we assume by contradiction that it is countable, and then we find an inconsistency with the diagonal argument. By contrast, when we show that A_TM is undecidable, we are not assuming countability of the set of languages by contradiction, because that is already true! Instead, we're assuming by contradiction the existence of an oracle. So in this case, we use the contradiction with a diagonal argument to disprove the existence of an oracle.

---

Halt_TM Is Undecidable

We can now talk about the problem that everyone mentions as the canonical undecidable problem: the halting problem:

Halt_TM = {<M,w> | M is a Turing machine and M halts (either accepts or rejects, but does not loop) on the string w}

Personally, I think A_TM is easier to use as the canonical undecidable problem, but it doesn't matter, because it's relatively straightforward to reduce A_TM to the halting problem. We will use the following theorem to our advantage

Let's use this strategy to prove that Halt_TM is undecidable. We'll use A_TM as problem A and Halt_TM as problem B. If we assume by contradiction that Halt_TM is decidable, then there must exist a decider machine H for this problem. We can use H to define the following machine to decide A_TM

This is, of course, a contradiction, since we know that A_TM is undecidable. Therefore, our assumption that Halt_TM is decidable is false, so Halt_TM must be undecidable.

---

E_TM Is Undecidable

A lot of times the halting problem is stated as the be all end all of undecidability. But there are (sadly) so many other useful problems that we cannot hope to solve in general. Let's now consider one called E_TM, which is the Turing machine equivalent of E_DFA and E_CFG

E_TM = {<M> | M is a Turing machine that does not accept anything}

Claim: E_TM is undecidable

Proof: We'll follow the same strategy by assuming by contradiction that E_TM is decidable. Let's say we have a decider machine E for this language, which we'll use to create a machine to decide A_TM. To do this, let's define a third machine that will help us:

This is kind of a weird trick, but we've defined a machine EmptyIndicator_M_w whose definition depends on a machine M and a string w, so the machine will actually change for a different M and w. But when we fix M and w, we see that the language L(EmptyIndicator_M_w) is empty if M does not accept w, or it consists of a single string "CS 373 Rocks" if M does accept w. Therefore, we can create a decider for A_TM by using E_TM's decider E

Since we know that A_TM is undecidable, we've reached a contradiction, and E_TM must not be decidable.

The thing that's weird about this proof is that the machine EmptyIndicator_M_w does not have to be a decider for us to decide whether it's empty by our assumption; we assumed that E_TM can decide whether any machine is empty. And this was enough for us to complete the proof by contradiction.

---

Reg_TM Is Undecidable

There's another fact we might love to know about a Turing machine we have (or about a computer program that we have, as per the Church-Turing Thesis): did we go way overkill but it can actually just be implemented as a DFA? This machine could have solved problem 5 on homework 6 with the "broken Turing machines," for example. For a more specific example, let's consider the following Turing machine:

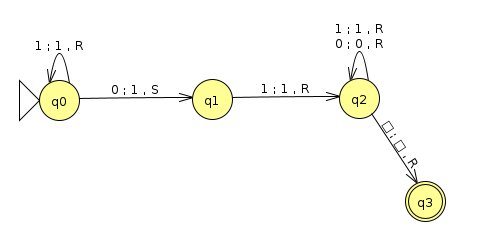
This Turing machine decides the language of binary strings with at least one 0. But this can be implemented more simply by just using a DFA

Let's now state the language in question more formally

Reg_TM = {<M> | M is a Turing machine and the language L(M) generated by M can be recognized by a DFA}

Claim: Reg_TM is undecidable

Proof: As per procedure, we'll assume by contradiction that Reg_TM is decidable and use it to create a decider for A_TM. Let's assume a decider for Reg_TM is called R. We'll use a similar trick to the one we used for E_TM and design an auxiliary machine that we'll eventually feed to Reg_TM

When we fix M and w, we see that the language L(RegIndicator_M_w) happens to be regular if M accepts w, or it happens to be nonregular if M does not accept w. Therefore, we can create a decider for A_TM by using Reg_TM's decider R on RegIndicator_M_w

We know A_TM is undecidable, so we've reached a contradiction, and Reg_TM must be undecidable as well.

---

TwoWrite_TM Is Undecidable

Let's consider one more language for good measure. Suppose we have a 2-tape turing machine. Then we claim the language

TwoWrite_TM = {<M,w> | M is a 2-tape Turing machine that writes a non-blank symbol to its second tape while processing w}

is undecidable

Proof: We can create a fairly straightforward decider for A_TM if we assume by contradiction that TwoWrite_TM is decidable. Let's create an auxiliary "wrapper machine" TwoWrite_Accept_M for any single tape turing machine M. This machine runs M on an input as normal, and if M accepts w, then it writes a single 1 on the second tape. Hence, this machine writes a non-blank symbol on the second tape if and only if M accepts w. Written out in pseudocode, we have:

Used to decide A_TM, we then have

Hence, TwoWrite_TM cannot be decidable.

---

Rice's Theorem

It may seem like we keep doing a similar thing for all of these problems, and we'd be able to save ourselves some work if we came up with a more general theorem for a class of undecidable languages that all have certain things in common. Here, we'll explore one such theorem known as Rice's Theorem.

Another way to understand Rice's theorem in the context of programming languages is that it is impossible to devise a decider for programs with a particular nontrivial semantic/behavioral property, ignoring the actual syntax of the programs that have this property. So we see, for example, that Rice's theorem applies to E_TM and Reg_TM, but Rice's theorem does not apply to TwoWrite_TM, since there are certainly ways to implement the same recognizer for a language without using a second tape, as we explained in the multitape to single tape reduction in class. Still, it could have saved us work on E_TM and Reg_TM.

Proof of Rice's Theorem: Let's assume the language P satisfying these two conditions is decidable. We have to somehow use the nontrivial and semantic properties of its language to create a decider for A_TM. Since it's nontrivial, we can assume there is at least one machine T whose encoding is in P, and at least one machine F whose encoding is not in P. Let's create the following auxiliary machine

Now let's let the machine M_P be a decider for our assumed decidable language P. Then the following machine decides A_TM

We've setup our auxiliary machine P_M_w to act like a machine in P if and only if M accepts w. Otherwise, it acts like a machine not in P. Therefore, M_p accepts P_M_w if and only if M accepts w. Therefore, we have created a decider for A_TM, which is a contradiction, showing that P is undecidable. This completes the proof.

We can see that some of the above examples use this logic directly. For instance, Reg_TM creates an auxiliary machine that acts like DFA if M accepts w, but which otherwise acts like a CFG, which is not in Reg_TM. But now we don't have to think so hard, and we just have to convince ourselves that there is at least one machine in the language and at least one machine not in the language, and that this property is a semantic property.

---

Co-Recognizable And Unrecognizable Languages

There's one more thing worth mentioning about undecidable languages: they don't play nicely with complements.

A language is called co-recognizable if its complement is recognizable. We can prove the following theorem about decidable languages:

Proof: Let's prove the first direction: that if a language is decidable, then it is recognizable and co-recognizable. We already know that if a language is decidable, then it's recognizable (since decidability is a stronger condition that rules out infinite loops). To show that it's also co-recognizable, we simply flip the Accept/Reject states, which we can safely do because there are no infinite loops.

Let's now prove the other direction: that if a language is both recognizable and co-recognizable, then it is decidable. In this case, we can assume that we have machines M_L and M_C that recognize a language and its complement, respectively. So we'll run M_L and M_C in parallel. If M_L accepts, then we accept. If M_C accepts, then we reject (since if a string is in the complement, it should not be in our language). Since these are both recognizers and they accept the opposite of each other, exactly one of them will accept eventually, even if the other loops infinitely. So we have a valid decider. This completes the proof.

This theorem tells us that complements play nicely with decidable languages, but they may not with undecidable languages.

The complement of A_TM Is Not Even Recognizable

Proof: Suppose by contradiction that the complement of A_TM is recognizable. Then both A_TM and its complement are recognizable, so by the above theorem, A_TM must be decidable. But the very first thing we talked about in these notes is that A_TM is not decidable. Therefore, the complement of A_TM must not even be recognizable! This completes the proof.

But wait, you may be saying! I can create a recognizer for the complement of A_TM using a recognizer A for A_TM as follows

Doesn't this recognize the complement of A_TM? Well, in order to recognize a language, we have to always be able to get to an accept state without infinitely looping. However, if A does not accept w, it may infinitely loop on it. So we might never get past the first if statement. This is intuitively why the complement of A_TM is not recognizable (but again, we need the rigorous proof above to rule out all ways of being clever).