Week 4: Efficiently Evaluating NFAs in Python

Chris Tralie

No Lambda Transitions

Let's start with the case of no λ transitions, as that will be easier to handle, and it matches the formal definition we gave for NFAs. Code is shown below:

?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
def eval_nfa(s, q, delta, F, verbose=False):
    """
    Evaluate a standard NFA with no lambda arrows
     
    Parameters
    ----------
    s: string
        Input to try
    q: string
        Start state
    delta: (string, string) -> set([string])
        Transition function
    F: set([string])
        Accept states
    verbose: bool
        If True, print info about sequence of states that are visited
    """
    states = set([q]) ## We now track multiple possibilities
    if verbose:
        print("Start", states)
    for c in s:
        next_states = set([])
        for p in states:
            if (p, c) in delta:
                ## This line is different from DFA; there are multiple
                ## states we can branch out to; track the unique ones
                next_states = next_states.union(delta[(p, c)])
        states = next_states
        if verbose:
            print(c, states)
    ## At least one state must be in the set of accept states F
    return len(states.intersection(F)) > 0

This code is quite similar to the DFA evaluation code we wrote, except the state transitions map onto a set of states. Likewise, we keep track of a set of states during the evaluation of the machine to keep track of the unique parallel universes we're considering. Finally, we accept if at least one state is in the set of accept states F.

As an example, let's return to the NFA that accepts strings that have a 1 in the 2's place:

?
1
2
3
4
5
6
7
8
9
10
11
delta = {
    ("q", "0"):{"q"},
    ("q", "1"):{"q", "q2"},
    ("q2", "0"):{"q0"},
    ("q2", "1"):{"q0"}
}
 
F = {"q0"}
q = "q"
s = "11010"

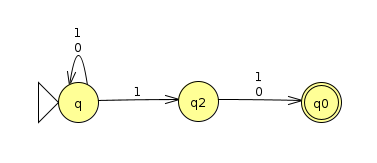
If we evaluate it

?
1
2
print(s, "Accepts:", eval_nfa(s, q, delta, F, verbose=True))

then it prints the following:

?
1
2
3
4
5
6
7
8
Start {'q'}
1 {'q2', 'q'}
1 {'q2', 'q0', 'q'}
0 {'q0', 'q'}
1 {'q2', 'q'}
0 {'q0', 'q'}
11010 Accepts: True

This matches the picture we drew

Reducing Lambda Transitions

The above code is useful for the textbook definition of NFAs, but as we've seen, adding λ transitions can make it much easier to specify certain NFAs, and this will be crucial for us on the next assignment when we create grep(1)

First, let's talk about how to represent λ transitions in python. Let's start with the union example from before. We'll use python None to represent λ, as shown below

?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
delta = {
    ("q", None):{"q0", "peven"},
     
    ("q0", "0"):{"q0"},
    ("q0", "1"):{"q1"},
    ("q1", "0"):{"q1"},
    ("q1", "1"):{"q2"},
    ("q2", "0"):{"q2"},
    ("q2", "1"):{"q2"},
     
    ("peven", "0"):{"podd"},
    ("peven", "1"):{"peven"},
    ("podd", "0"):{"peven"},
    ("podd", "1"):{"podd"}
}
q = "q"
F = {"q0", "q1", "podd"}
s = "00011"

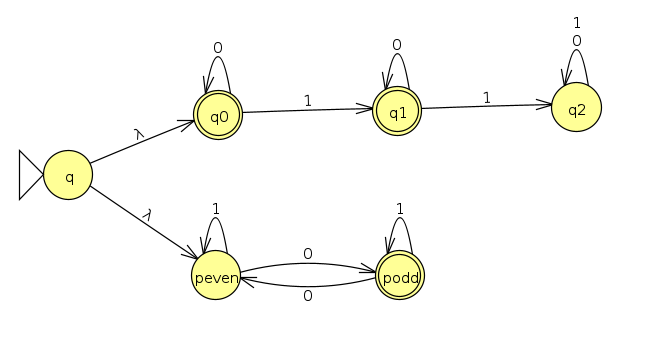
Now, rather than rewriting our code to evaluate NFAs, we'll do the reduction from NFAs with λ to those without so we can use the evaluation code we already have. First, we'll create a helper method to figure out which states are reachable from a particular state via a sequence of λ transitions. To accomplish this, we'll use depth-first graph search:

?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
def get_reachable_lambdas(start, delta):
    """
    Parameters
    ----------
    start: string
        State at which to start.  We'll gather anything
        that can be reached by a sequence of lambdas
        from this state
    delta: (string, string) -> set([string])
        Transition function
     
    Returns
    -------
    set([string])
        Set of all states reachable from start
        by a sequence of lambda arrows
    """
    reachable = set([])
    stack = [start]
    while len(stack) > 0:
        state = stack.pop()
        reachable.add(state)
        if (state, None) in delta:
            # If there are lambda arrows out of this state,
            # loop through all of them
            for neighbor in delta[(state, None)]:
                if not neighbor in reachable:
                    # If we haven't seen this state yet
                    # (Crucial to avoid infinite loops for lambda cycles)
                    stack.append(neighbor)
    reachable.remove(start) # Exclude the start state itself
    return reachable

Let's look at the crazy example we had from before:, but we'll add one more λ transition from q3 to q1 to create a cycle, just to make sure we can handle that

?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
delta = {
    ("q0", "0"):{"q0"},
    ("q0", None):{"q1"},
     
    ("q1", "0"):{"q1"},
    ("q1", "1"):{"q3"},
    ("q1", None):{"q2"},
     
    ("q2", "0"):{"q2"},
    ("q2", "1"):{"q1"},
    ("q2", None):{"q3"},
     
    ("q3", "0"):{"q3"},
    ("q3", None):{"q1"}
}

If we check the method we just made on all the states

?
1
2
3
for state in ["q0", "q1", "q2", "q3"]:
print(state, get_reachable_lambdas(state, delta))

then we get this:

?
1
2
3
4
5
q0 {'q1', 'q2', 'q3'}
q1 {'q2', 'q3'}
q2 {'q1', 'q3'}
q3 {'q1', 'q2'}

which is correct. Let's finish the reduction now by adding non-lambda arrows out of the reachable states to each state, and by updating the accept states

?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
def reduce_nfa_lambdas(delta, F):
    """
    Eliminate the lambdas in an NFA by doing a reduction
    to equivalent arrows and accept states to without
    lambdas
     
    Parameters
    ----------
    delta: (string, string) -> set([string])
        Transition function, which will be updated as as side effect
    F: set([string])
        Final states, which will be updated as as side effect
    """
    ## Step 1: Copy the dictionary into a new format where
    ## it's more convenient to look up only the arrows coming
    ## out of a particular state
    delta_state = {} #(State):(Character:set(states))
    for (state, c), states_to in delta.items():
        if not state in delta_state:
            delta_state[state] = {}
        if not c in delta_state[state]:
            delta_state[state][c] = set([])
        delta_state[state][c].update(states_to)
 
    ## Step 2: Loop through each state, get the new arrows, and
    ## update the final states
    states = set([key[0] for key in delta])
    F_new = set([])
    for state in states:
        # Get states that are reachable from this state
        reachable = get_reachable_lambdas(state, delta)
        # Figure out if this should be an accept state based
        # on what's reachable
        if len(reachable.intersection(F)) > 0:
            F_new.add(state)
        # Add the new arrows
        for other in reachable:
            if other in delta_state: # If there are actually any arrows coming out of this state
                for c, states_to in delta_state[other].items():
                    if c is not None:
                        # Add this new equivalent arrow
                        if not (state, c) in delta:
                            delta[(state, c)] = set([])
                        delta[(state, c)] = delta[(state, c)].union(states_to)
    F.update(F_new)
     
    ## Step 3: Remove the original lambda arrows
    to_remove = [key for key in delta.keys() if key[1] is None]
    for key in to_remove:
        del delta[key]

Let's run this code on the example we have and see what we get:

?
1
2
3
4
5
reduce_nfa_lambdas(delta, F)
for key in sorted(delta.keys()):
    print(key, ":", sorted(delta[key]))
print("F", sorted(F))
?
1
2
3
4
5
6
7
8
9
10
11
('q0', '0') : ['q0', 'q1', 'q2', 'q3']
('q0', '1') : ['q1', 'q3']
('q1', '0') : ['q1', 'q2', 'q3']
('q1', '1') : ['q1', 'q3']
('q2', '0') : ['q1', 'q2', 'q3']
('q2', '1') : ['q1', 'q3']
('q3', '0') : ['q1', 'q2', 'q3']
('q3', '1') : ['q1', 'q3']
F ['q0', 'q1', 'q2', 'q3']

The new transitions and new accept states are depicted in red. We've added lots of arrows, but it seems our code has worked correctly! This is a useless example in practice since every state accepts (since every state can reach q2 with a sequence of λ transitions), but it was good to test our code on

Union Example Again

Now let's go back to the union example and see what we get:

?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
delta = {
    ("q", None):{"q0", "peven"},
      
    ("q0", "0"):{"q0"},
    ("q0", "1"):{"q1"},
    ("q1", "0"):{"q1"},
    ("q1", "1"):{"q2"},
    ("q2", "0"):{"q2"},
    ("q2", "1"):{"q2"},
      
    ("peven", "0"):{"podd"},
    ("peven", "1"):{"peven"},
    ("podd", "0"):{"peven"},
    ("podd", "1"):{"podd"}
}
q = "q"
F = {"q0", "q1", "podd"}
s = "00011"
  
reduce_nfa_lambdas(delta, F)
print(s, "Accepts:", eval_nfa(s, q, delta, F, verbose=True))

And we get

?
1
2
3
4
5
6
7
8
9
Start {'q'}
0 {'podd', 'q0'}
0 {'q0', 'peven'}
0 {'podd', 'q0'}
1 {'podd', 'q1'}
1 {'podd', 'q2'}
00011 Accepts: True

This accepts because even though in one of the unique parallel universes it ends on q2, in the other one, it ends on podd, an accept state

Messy Lambda Clone Example

Finally, let's go back and look at this example

?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
delta = {
    ("q0", None):{"q1"},
    ("q0", "0"):{"q0"},
    ("q0", "1"):{"q1"},
      
    ("q1", "1"):{"q1"},
    ("q1", None):{"q2"},
      
    ("q2", "0"):{"q2"}
}
q = "q0"
F = {"q2"}
  
reduce_nfa_lambdas(delta, F)
print("0011", "Accepts:", eval_nfa(s, q, delta, F, verbose=True))

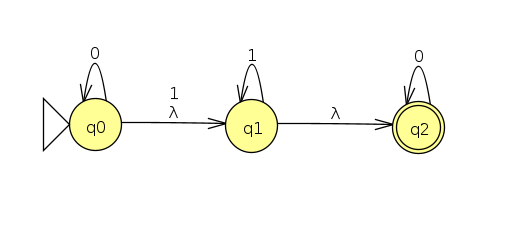
We get the output below, which matches the picture we drew before on the right; that is, we end up in state q1, which is adjacent to q2 by a λ arrow, so we accept.

Note that the NFA transitions on our reduced machine do not immediately show the λ clones in the verbose output, but they are behaving correctly.

?
1
2
3
4
5
6
7
8
Start {'q0'}
0 {'q2', 'q0'}
0 {'q2', 'q0'}
0 {'q2', 'q0'}
1 {'q1'}
1 {'q1'}
0011 Accepts: True                                             

Seems like everything is working well! Feel free to use this code on the grep part of HW4.

Footnote 1

Brian Kernighan made this video at around the time I had him as an academic adviser at Princeton, so that's how I remember him. His advice to me at the time was to take more theory courses (up to the point that we met I'd done mostly applications like music, graphics, and human computer interface). He was right! Theory is now also a huge passion of mine, as evidenced by these notes. I am eternally grateful for that push he gave me.

If there's one more thing I could go back and tell myself, it would be that it's OK if you struggle with the stuff at first, that's normal. Keep trying, and it will be amazing.